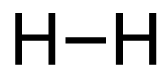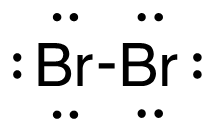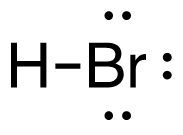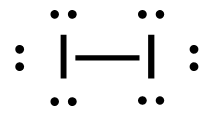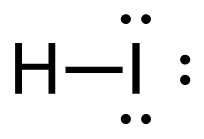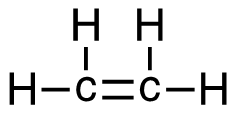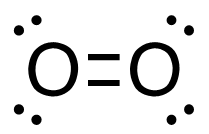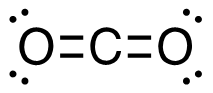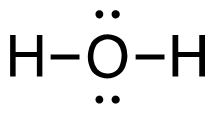Chemical Bonding — Basic Concepts: Calculate Enthalpy Change from Bond Energy

Question

Using the bond energies in Table 4.6.1: Bond Energies (kJ/mol) from Section 4.6: Strengths of Ionic and Covalent Bonds (1), determine the approximate enthalpy change for each of the following reactions:

  1. H2(g) + Br2(g) → 2HBr(g)
  2. CH4(g) + I2(g) → CH3I(g) + HI(g)
  3. C2H4(g) + 3O2 → 2CO2(g) + 2H2O(g)

 

Show/Hide Answer
  1. −114 kJ
  2. 30. kJ
  3. −1055 kJ

Refer to Section 4.6: Strengths of Ionic and Covalent Bonds (1).

Strategy Map

Do you need a little help to get started?

Check out the strategy map.

Show/Hide Strategy Map
Table 1: Strategy Map
Strategy Map Steps
1. Identify which molecules have bonds broken and which have bonds formed.

Show/Hide Hint

Reactant bonds break, and product bonds form in a chemical reaction.
2. Create Lewis structures for each of the molecules to know what bonds there are.

Show/Hide Hint

If you are unsure which elements are bonded to which, try making a Lewis Structure of the molecule.

Refer to Section 4.4 Lewis Symbols and Structures (2).
3. Use the provided table to look up the corresponding bond energies.

Show/Hide Hint

Table 4.6.1: Bond Energies (kJ/mol) from Section 4.6: Strengths of Ionic and Covalent Bonds (1).
4. Plug the values into the enthalpy change equation and solve for each reaction.

Show/Hide Hint

Breaking bonds requires an energy input. When bonds form, energy is released. When energy is released, it is negative. Recall the equation that demonstrates this relationship.

Solution

Do you want to see the steps to reach the answer?
Check out this solution. 

Show/Hide Solution 

1. H2 (g) + Br2 (g) → 2HBr (g)

[latex]\begin{align} \Delta& \mathrm{H}=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right) \\\\ \Delta& \mathrm{H}=(1(\mathrm{H-H})+1(\mathrm{Br-Br}))-(2(\mathrm{H-Br})) \\\\ \Delta& \mathrm{H}=(1 \mathrm{~mol}(436\mathrm{~kJ}/ \mathrm{mol})+1\mathrm{~mol}(190. \mathrm{~kJ}/\mathrm{mol}))-(2 \mathrm{~mol}(370. \mathrm{~kJ}/ \mathrm{mol})) \\\\ \Delta& \mathrm{H}=(626 \mathrm{~kJ})-(740. \mathrm{~kJ}) \\\\ \Delta& \mathrm{H}=-114 \mathrm{~kJ} \end{align}[/latex]

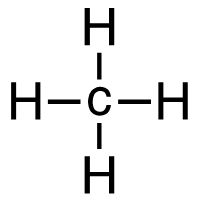
2. CH4 (g) + I2 (g) → CH3I (g) + HI (g)

[latex]\begin{align} \Delta& \mathrm{H}=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right) \\\\ \Delta& \mathrm{H=(4(C-H)+(I-I))-(3(C-H)+(C-I)+(H-I))} \\\\ \Delta& \mathrm{H=(4~mol(415 ~kJ/mol)+1~mol(150. ~kJ/mol))-(3~mol(415 ~kJ/mol)\\+1~mol(240. ~kJ/mol)+1~mol(295 ~kJ/mol))} \\\\ \Delta& \mathrm{H=(1660~kJ+150. ~kJ)-(1245 ~kJ + 240. ~kJ + 295 ~kJ)} \\\\ \Delta& \mathrm{H=(1810 ~kJ)-(1780 ~kJ)} \\\\ \Delta& \mathrm{H}=\mathrm{30.} \mathrm{~ kJ} \end{align}[/latex]

3. C2H4 (g) + 3O2 (g)→ 2CO2 (g) + 2H2O (g)

[latex]\begin{align} \Delta& \mathrm{H}=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right) \\\\ \Delta& \mathrm{H=(4(C-H)+(C=C)+3(O=O))-(2(2(C=O))+2(2(H-O)))} \\\\ \Delta& \mathrm{H=(4 ~mol(415 ~kJ/mol)+1 ~mol(611 ~kJ/mol)+3~mol(498 ~kJ/mol))\\-(4 mol(741 ~kJ/mol)+4 ~mol(464 ~kJ/mol))} \\\\ \Delta& \mathrm{H=((1660 ~kJ + 611 ~kJ) + (1494 ~kJ - 2964 ~kJ + (1856 ~kJ)} \\\\ \Delta& \mathrm{H=(3765 ~kJ)-(4820 ~kJ)} \\\\ \Delta& \mathrm{H}=-\mathrm{1 0 5 5} \mathrm{~kJ} = 1.05_5\mathrm{x}10^3\mathrm{~kJ} \end{align}[/latex]

Guided Solution

Do you want more help?
The guided solution below will give you the reasoning for each step to get your answer, with reminders and hints.

Show/Hide Guided Solution
Table 2: Guided Solution
Guided Solution Ideas
This question is a calculation problem in which you must identify what bonds are broken and formed during a chemical reaction. This type of problem requires you to use a table of values to calculate the overall energy change in the reaction using bond energies.

Show/Hide Resource

Refer to Section 4.6: Strengths of Ionic and Covalent Bonds (1).
It can be difficult to know how many bonds are in a molecule. The easiest way to find what bonds there are is to create a Lewis Structure of the molecule.

Show/Hide Resource

Refer to Section 4.4 Lewis Symbols and Structures (2).

1. H2 (g) + Br2 (g) → 2HBr (g)

Create Lewis structures for H2, Br2 and HBr.

Show/Hide Structures 

 

2 hydrogen atoms connected by a covalent bond.

2 bromine atoms, with 6 electrons each, connected by a covalent bond.

A bromine atom with 6 electrons connected to a hydrogen atom by a covalent bond.

2. CH4 (g) + I2 (g) → CH3I (g) + HI (g)

Create Lewis structures for CH4, I2, CH2I and HI.

Show/Hide Structures

1 carbon atom connected to 4 hydrogen atoms by covalent bonds.

2 iodine atoms, with 6 electrons each, connected by a covalent bond.

One carbon atom surrounded by 3 hydrogen atoms and 1 iodine atom (with 6 electrons), which all connect to the carbon through covalent bonds.

1 iodine atom, with 6 electrons, connected to a hydrogen atom by a covalent bond.

3. C2H4 (g) + 3O2 (g) → 2CO2 (g) + 2H2O (g)

Create Lewis structures for C2H4, O2, CO2 and H2O.

Show/Hide Structures

2 carbon atoms that each have 2 hydrogen atoms attached to the through covalent bonds. The 2 carbon atoms are connected via a double bond.

2 oxygen atoms, with 4 electrons each, connected by a double covalent bond.

2 oxygen atoms, with 4 electrons each, both connect to a carbon atom through double covalent bonds.

2 hydrogen atoms connect to 1 oxygen atom (with 4 electrons) by covalent bonds.
Recall that bonds require energy to break (start a reaction), and energy is released when bonds form (in the products of a reaction).

Show/Hide Don’t Forget!

[latex]\Delta H=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right)[/latex]

The energy of bonds formed is subtracted as they are formed in the reaction. Bond energy values, by definition, are the energy required to break the bond. By subtracting the sum of the product bonds formed, we are changing the sign of the energy to represent the opposite process (forming the bond).
When using the bond energies table, scan the table for your desired bond (i.e. (H-H)). The number beside it will be the one used in the calculation. Make sure you don’t confuse single, double, and triple bonds!

Show/Hide Don’t Forget!

The bond energy for H-H is 436 kJ.
Table 3: Complete Solution
Complete Solution
The following equation will be used for each of the reactions:

[latex]\Delta H=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right)[/latex]

For a reaction to occur, bonds need to break, and new bonds need to form. When bonds break, energy is absorbed. When bonds form, energy is released. We use this to calculate the sum of the energy change over the reaction. How do we know which bonds are breaking and which are forming?

Show/Hide Don’t Forget!

In a reaction, the bonds to the left of the arrow will break, and the bonds to the right will form.

___(break)___ → ___(form)___
1. H2 (g) + Br2 (g) → 2HBr (g)

[latex]\Delta H=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right)[/latex]

The bond between the two hydrogen and the two bromine atoms breaks. Two product molecules form, each with a hydrogen bonded to a bromine.

Show/Hide Structures

2 hydrogen atoms connected by a covalent bond.

2 bromine atoms, with 6 electrons each, connected by a covalent bond.

A bromine atom with 6 electrons connected to a hydrogen atom by a covalent bond.

[latex]\Delta \mathrm{H}=(1 \operatorname{mol}\mathrm{(H-H)+1} \operatorname{mol}\mathrm{(B r-B r))-(2} \operatorname{mol}\mathrm{(H-B r))}[/latex]

Using Table 4.6.1: Bond Energies (kJ/mol) from Section 4.6: Strengths of Ionic and Covalent Bonds (1), the values for each bond energy replaces their respective bonds in the equation.

[latex]\Delta \mathrm{H=(1} \mathrm{~mol}(436 \mathrm{~kJ} / \mathrm{mol})+1 \mathrm{~mol}(190 . \mathrm{kJ} / \mathrm{mol}))-(2 \mathrm{~mol}(370 . \mathrm{kJ} / \mathrm{mol}))[/latex]

When solving inside the brackets, keep stoichiometry in mind.

[latex]\Delta \mathrm{H=(626 k J)-(740 . k J)}[/latex]

The energy released from the bonds formed is subtracted from the energy absorbed by the bonds broken.

ΔH=-114 kJ

The calculated value is negative, meaning the reaction was exothermic.
2. CH4 (g) + I2 (g) → CH3I (g) + HI (g)

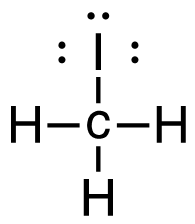
[latex]\Delta \mathrm{H}=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right)[/latex]

Four carbon-hydrogen and one iodine-iodine bonds break. Three carbon-hydrogen bonds, one carbon-iodine and one hydrogen-iodine, are formed.

Show/Hide Think About This!

Make sure you have the correct bonds for CH4 and CH3I.

Show/Hide Structures

1 carbon atom connected to 4 hydrogen atoms by covalent bonds.

2 iodine atoms, with 6 electrons each, connected by a covalent bond.

One carbon atom surrounded by 3 hydrogen atoms and 1 iodine atom (with 6 electrons), which all connect to the carbon through covalent bonds.

1 iodine atom, with 6 electrons, connected to a hydrogen atom by a covalent bond.

[latex]\Delta \mathrm{H=(4(C-H)+(I-I))-(3(C-H)+(C-I)+(H-I))}[/latex]

Using Table 4.6.1: Bond Energies (kJ/mol) from Section 4.6: Strengths of Ionic and Covalent Bonds (1), the values for each bond energy replaces their respective bonds in the equation.

[latex]\begin{align} \Delta& \mathrm{H=(4mol(415 kJ/mol)+1 mol(150. kJ/mol))-(3 mol(415 kJ/mol)\\+1 mol(240. kJ/mol)+1 mol(295 kJ/mol))} \\\\ \Delta& \mathrm{H=((1660 kJ)+(150. kJ))-((1245 kJ)+(240. kJ)+(295 kJ))} \end{align}[/latex]

When solving inside the brackets, keep stoichiometry in mind.

[latex]\Delta \mathrm{H=(1810 kJ)-(1780 kJ)}[/latex]

The energy released from the bonds formed is subtracted from the energy absorbed by the bonds broken.

ΔH=30 kJ

The calculated value is positive, meaning the reaction was endothermic
3. C2H4 (g) + 3O2 (g) → 2CO2 (g) + 2H2O (g)

[latex]\Delta \mathrm{H}=\left(\sum \text { Bonds broken }\right)-\left(\sum \text { Bonds formed }\right)[/latex]

Two hydrogen-carbon, one carbon-carbon double, and three oxygen-oxygen double bonds break. Two molecules of CO2 form that contain two carbon-oxygen double bonds and two molecules, each containing two hydrogen-oxygen bonds.

Show/Hide Think About This!

Make sure you have the correct bonds for C2H4, O2 and CO2.

Show/Hide Structures

2 carbon atoms that each have 2 hydrogen atoms attached to the through covalent bonds. The 2 carbon atoms are connected via a double bond.

2 oxygen atoms, with 4 electrons each, connected by a double covalent bond.

2 oxygen atoms, with 4 electrons each, both connect to a carbon atom through double covalent bonds.

2 hydrogen atoms connect to 1 oxygen atom (with 4 electrons) by covalent bonds.

[latex]\begin{gathered} \Delta \mathrm{H=(4(C-H)+(C=C)+3(O=O))-(2(2(C=O))+2(2(H-O)))} \end{gathered}[/latex]

Using Table 4.6.1: Bond Energies (kJ/mol) from Section 4.6: Strengths of Ionic and Covalent Bonds (1), the values for each bond energy replaces their respective bonds in the equation.

[latex]\begin{gathered} \Delta \mathrm{H=(4 mol(415 kJ/mol)+1 mol(611 kJ/mol)\\ +3 mol(498 kJ/mol))-(4 mol(741 kJ/mol)\\ +4 mol(464 kJ/mol))} \end{gathered}[/latex]

When solving inside the brackets, keep stoichiometry in mind.

[latex]\begin{align} \Delta& \mathrm{H=((1660 kJ)+(611 kJ)+(1494 kJ))-((2964 kJ)+(1856 kJ))} \\\\ \Delta& \mathrm{H=(3765 kJ)-(4820 kJ)} \end{align}[/latex]

The energy released from the bonds formed is subtracted from the energy absorbed by the bonds broken.

ΔH= -1055 kJ = 1.055 x 103 kJ

The calculated value is negative, meaning the reaction was exothermic.

Check Your Work

When comparing the bond energy values, we see that the product bonds (2 H-Br) have a greater magnitude than the reactant bonds (H-H and Br-Br), so we would expect this reaction to have an exothermic ΔH.

Show/Hide Watch Out! 

Make sure you add up all bonds and consider the reaction stoichiometry.

Does your answer make chemical sense?

Show/Hide Answer 

When any reaction occurs, energy will be absorbed and released; however, the overall sum can be endothermic (requires more energy than it releases) or exothermic (releases more energy than it requires). We can numerically observe this using the enthalpy change from the bond energies equation.

PASS Attribution

Media Attributions

  • Figures 1 to 11 by the authors (Brewer S. and Blackstock L.) are free to use under a CC0 license.

References

1. OpenStax. 4.6: Strengths of Ionic and Covalent Bonds. In CHEM1500: Chemical Bonding and Organic Chemistry. LibreTexts, 2022. https://chem.libretexts.org/Courses/Thompson_Rivers_University/CHEM1500%3A_Chemical_Bonding_and_Organic_Chemistry/04%3A_Chemical_Bonding_I-_Basic_Concepts/4.06%3A_Strengths_of_Ionic_and_Covalent_Bonds.

2. OpenStax. 4.4: Lewis Symbols and Structures. In CHEM1500: Chemical Bonding and Organic Chemistry. LibreTexts, 2022. https://chem.libretexts.org/Courses/Thompson_Rivers_University/CHEM1500%3A_Chemical_Bonding_and_Organic_Chemistry/04%3A_Chemical_Bonding_I-_Basic_Concepts/4.04%3A_Lewis_Symbols_and_Structures.

3. Blackstock, L.; Brewer, S.; Jensen, A. In PASS Chemistry Book CHEM 1510/1520; LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/PASS_Chemistry_Book_CHEM_1510%2F%2F1520.

4. Blackstock, L.; Brewer, S.; Jensen, A. 4.3: Question 4.E.65 PASS – determining enthalpy change from bond energies. In PASS Chemistry Book CHEM 1500. LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/PASS_Chemistry_Book_CHEM_1500/04%3A_Chemical_Bonding_I_-_Basic_Concepts/4.03%3A_Question_4.E.65_PASS_-_determining_enthalpy_change_from_bond_energies.

5. OpenStax. 7.E: Chemical Bonding and Molecular Geometry (Exercises). In Chemistry 1e (OpenSTAX). LibreTexts. 2022. https://chem.libretexts.org/Bookshelves/General_Chemistry/Chemistry_1e_(OpenSTAX)/07%3A_Chemical_Bonding_and_Molecular_Geometry/7.E%3A_Chemical_Bonding_and_Molecular_Geometry_(Exercises).

6. Flowers, P.; Theopold, K.; Langley, R.; Robinson, W. R. Ch. 7 Exercises. In Chemistry 2e. https://openstax.org/books/chemistry-2e/pages/7-exercises.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

PASSchem Copyright © by Sharon Brewer, Lindsay Blackstock, TRU Open Press is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book