Quantum Theory and Electronic Structure: Quantum Numbers, Orbital Characteristics

Question

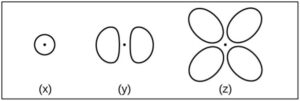
Consider the orbitals shown below…

 

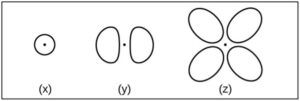
Three different orbital types listed as (x), (y) and (z). The orbital listed as (x) consists of one circle with a smaller, filled circle dot in the centre. The orbital listed as (y) consists of two large lobes on either side of a small dot and is dumbbell/propellor shaped. The orbital listed as (z) consists of four large lobes surrounding a smaller filled circle dot and is 4-leaf clover/daisy shaped.

  1. What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?
  2. How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?
  3. Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.
  4. What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?
  5. What are the possible l and ml values for an orbital of type (x)? Of type (y)? Of type (z)?

 

Show/Hide Answer
  1. Type (x) = 2 electrons
    Type (y) = 2 electrons
    Type (z) = 2 electrons
  2. Type (x) = 1 orbital
    Type (y) = 3 orbitals
    Type (z) = 0, does not exist
  3. Type (x) = [4, 0, 0, ½]
    Type (y) = [2, 1, 0, -½]
    Type (z) = [3, 2, -1, ½]
  4. Type (x): n = 1
    Type (y): n = 2
    Type (z): n = 3
  5. Type (x): l =0, ml =0
    Type (y): l = 1, ml = 1, 0, -1
    Type (z): l = 2, ml = 2, 1, 0, -1, -2

Refer to:

  • Figure 2.5.7 in Section 2.4: Quantum Mechanics and the Atom (1) for a visual representation of the orbital types and their suborbital positions.
  • Figure 2.6.3 in Section 2.6, Electronic Structure of Atoms (Electron Configurations) (2) for a visual representation of the hierarchy of subshell filling/energy levels.

Strategy Map

Do you need a little help to get started?

Check out the strategy map.

Show/Hide Strategy Map
Table 1: Strategy Map
Strategy Map Steps
1. Identify what orbital types are represented in the figure.

Show/Hide Hint

In general chemistry, 4 types of orbitals are introduced: s, p, d, and f.

Recall this mnemonic, where the letter can help describe the shape:

  • s  — sphere = 1 lobe
  • p — propeller = 2 lobes
  • d — daisy = 4 lobes; or donut = 2 lobes and a ring shape
  • f — funky = 7 lobes
2. Consider each requirement of this multi-part problem and work through the answer step by step to not miss anything.

Show/Hide Hint

Be familiar with the fundamental concepts of atomic orbital theory and the key characteristics of each orbital type.

Consider: Hund’s Rule, Aufbau’s Principle, and the Pauli Exclusion Principle to guide your thinking.

Solution

Do you want to see the steps to reach the answer?

Check out this solution.

Show/Hide Solution

All Types

a. What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?

Answer: Any orbital can house a total of 2 electrons (1 with spin up + ½ and 1 with spin down – ½).

Type (x)

The shape of this orbital is spherical (s-type; 1 lobe; no planar nodes).

s-type orbitals have the following characteristics:

  • n is equal to or greater than 1.
  • l is always equal to 0 (defines the shape).
  • ml is always equal to 0 (only 1 distinct orientation).
  • there is only ever 1 s-type orbital per n-level
  • ms can be equal to -½ or +½

Answers:

  1. 1 orbital
  2. [4, 0, 0, ½]
  3. n = 1
  4. l = 0, ml = 0

Type (y)

The shape of this orbital is a dumbbell or propellor (p-type; 2 lobes; 1 planar node in x-, y-, or z-axis).

p-type orbitals have the following characteristics:

  • n is equal to or greater than 2; p-type orbitals cannot exist when n = 1.
  • l is always equal to 1 (defines the shape).
  • ml can be -1, 0, or 1 (3 distinct orbital orientations).
  • there can be up to 3 p-type orbitals per n-level (when n is greater than or equal to 2).
  • ms can be equal to -½ or +½

Answers:

  1. 3 orbitals
  2. [2, 1, 0, -½]
  3. n = 2
  4. l = 1; ml = -1, 0, 1

Type (z)

The shape of this orbital is a clover or daisy (d-type; typically 4 lobes; typically 2 planar nodes).

d-type orbitals have the following characteristics:

  • n is equal to or greater than 3; d-type orbitals cannot exist when n = 1 or 2.
  • l is always equal to 2 (defines the shape).
  • ml can be -2, -1, 0, 1, or 2 (5 distinct orbital arrangements)
  • there can be up to 5 d-type orbitals per n-level (when n is greater than or equal to 3).
  • ms can be equal to -½ or +½.

Answers:

  1. 0 orbitals, does not exist
  2. [3, 2, -1, ½]
  3. n = 3
  4. l = 2, ml = 2, 1, 0, -1, -2

Guided Solution

Do you want more help?

The guided solution below will give you the reasoning for each step to get your answer, with reminders and hints.

Show/Hide Guided Solution
Table 2: Guided Solution
Guided Solution Ideas
This problem requires comprehension of the following concepts:

  • Quantum mechanics and the atom
  • Shapes of atomic orbitals
  • Electronic structure of atoms

Consider the orbitals shown below:

Orbital (x) consists of a single lobe and is sphere shaped, orbital (y) consists of two lobes and is dumbbell/propellor shaped, orbital (z) consists of four lobes and is 4-leaf clover/daisy shaped.

Show/Hide Resource

Refer to:
Recall the quantum numbers.

Show/Hide Don’t Forget!

Quantum numbers: [n, l, ml, ms]

What are the quantum numbers, and what do they represent? What are the guidelines/rules/principles that inform each quantum number?

Show/Hide Don’t Forget!
  • n (principal quantum number; represents shell energy level):
    • Must be a whole number integer (i.e., n = 1, 2, 3, … n)
    • Bigger number = greater energy = greater distance from nucleus = larger size
  • l (azimuthal/orbital angular momentum quantum number; represents orbital shape):
    • Must be 0 or a positive whole number integer; restricted by n (i.e., l = 0, 1, 2, … n-1; l≠n)
      • When l = 0, type s (sphere-shaped = 1 lobe)
      • When l = 1, type p (propeller-shaped = 2 lobes)
      • When l = 2, type d (daisy-shaped = 4 lobes; or donut-shaped = 2 lobes and a ring shape)
      • When l = 3, type f (funky-shaped = 7 lobes)
  • ml (magnetic quantum number; represents the orientation of the orbital within a subshell):
    • Must be a positive or negative whole number integer, or 0; restricted by l (i.e., ml = -l, … -2, -1, 0, 1, 2, … +l)
      • For s-type, l = 0; ml must be 0
      • For p-type, l = 1; ml can be -1, 0, or +1
      • For d-type, l = 2; ml can be -2, -1, 0, +1, or +2
  • ms (spin quantum number; represents the direction of spin of the electron):
    • Can be +½ OR -½; not restricted by any other quantum number.
Table 3: Complete Solution
Complete Solution
a. What is the maximum number of electrons contained in an orbital of type (x)? Of type (y)? Of type (z)?

Think about how many electrons can you put into any orbital. Think about electron pairing.

Regardless of orbital type, each orbital can contain at most 2 electrons; 1 electron spins in a direction (ms = +½), and the other electron spins in the opposite direction (ms=-½).

Answer:

  • Type (x) = 2 electrons
  • Type (y) = 2 electrons
  • Type (z) = 2 electrons
b. How many orbitals of type (x) are found in a shell with n = 2? How many of type (y)? How many of type (z)?

First, identify each orbital type based on the shape in the provided figure.

Here, we must consider what quantum numbers are allowed for each orbital type when n = 2.

  • Type (x) — 1 lobe; sphere-shaped (s); l = 0
  • Type (y) — 2 lobes; propeller-shaped (p); l = 1
  • Type (z) — 4 lobes; daisy-shaped (d); l = 2

Consider the relationship between quantum numbers n and l when n = 2; is each orbital type (i.e., x, y, and z) allowed?

Recall: l must be 0 or a positive whole number integer; restricted by n (i.e., l = 0, 1, 2, … n-1).

  • Type (x) — when n=2; l = 0 (allowed)
  • Type (y) — when n=2; l = 1 (allowed)
  • Type (z) — when n=2; l ≠ 2 (NOT allowed)

Summary: A Type (z) or ‘d-type’ orbital does not exist in the n = 2 shell.

Answer:

  • Type (x) = 1 orbital
  • Type (y) = 3 orbitals
  • Type (z) = 0 orbitals
c. Write a set of quantum numbers for an electron in an orbital of type (x) in a shell with n = 4. Of an orbital of type (y) in a shell with n = 2. Of an orbital of type (z) in a shell with n = 3.

Consider what each quantum number represents.

Summarize the quantum numbers you have been provided in the question.

Recall there are 4 distinct quantum numbers [n, l, ml, ms].

The question provides the principal quantum number (n), and the shape of the orbital defines the angular momentum quantum number (l):

  • Type (x) — [n = 4, l = 0]
  • Type (y) — [n = 2, l = 1]
  • Type (z) — [n = 3, l = 2]

What quantum numbers must be defined to answer the question? Are there any restrictions that must be considered?

Still need ml and ms:

  • ml must be a positive or negative whole number integer, or 0; restricted by l (i.e., ml = -l, … -2, -1, 0, 1, 2, … +l)
  • ms can be +½ OR -½; not restricted by any other quantum number

Is there more than one correct answer? Yes, there is more than one allowed quantum number set for each orbital type, as defined in the question.

Type (x) = [n = 4, l = 0, ml = 0, ms = +½]

  • ml must equal 0 because l = 0
  • ms = -½ would also be allowed
    • 2 correct answers
    • The 4s orbital can hold 2 electrons; each electron has a unique set of 4 quantum numbers

Type (y) = [n = 2, l = 1, ml = 0, ms = -½]

  • ml = -1 and ml = +1 would also be allowed.
  • ms = +½ would also be allowed.
    • 6 correct answers
    • The 2p orbitals can hold 6 total electrons; each electron has a unique set of 4 quantum numbers
      • 2 electrons in each px, py, and pz

Type (z) = [n = 3, l = 2, ml = -1, ms = +½]

  • ml = -2, 0, +1, and +2 would also be allowed.
  • ms = -½ would also be allowed.
    • 10 correct answers
    • The 3d orbitals can hold 10 total electrons; each electron has a unique set of 4 quantum numbers
      • 2 electrons in each dxy, dyz, dxz, dx2–y 2 and dz2

Answer:

  • Type (x) = [4, 0, 0, ½]
  • Type (y) = [2, 1, 0, -½]
  • Type (z) = [3, 2, -1, ½]
d. What is the smallest possible n value for an orbital of type (x)? Of type (y)? Of type (z)?

Consider the relationship between quantum numbers n and l.

Recall: l must be 0 or a positive whole number integer; the value of l is restricted by n (i.e., l = 0, 1, 2, … n-1; l≠n).

Therefore, the lowest value of n = (l + 1).

Recall the value of l for each type of orbital:

  • Type (x) — 1 lobe; sphere-shaped (s); l = 0
  • Type (y) — 2 lobes, propeller-shaped (p); l = 1
  • Type (z) — 4 lobes, daisy-shaped (d); l = 2

Using those l values, you can calculate the lowest n for each type:

  • Type (x) — lowest n = (l + 1) = (0 + 1) = 1
  • Type (y) — lowest n = (l + 1) = (1 + 1) = 2
  • Type (z) — lowest n = (l + 1) = (2 + 1) = 3

Answer:

  • Type (x) — n = 1
  • Type (y) — n = 2
  • Type (z) — n = 3
e. What are the possible l and ml values for an orbital of type (x)? Of type (y)? Of type (z)?

Consider the relationship between ml and l quantum numbers.

ml must be a positive or negative whole number integer, or zero; ml is restricted by l (i.e., ml = -l, … -2, -1, 0, 1, 2, … +l).

Recall the value of l for each type of orbital:

  • Type (x) — 1 lobe; sphere-shaped (s); l = 0
  • Type (y) — 2 lobes, propeller-shaped (p); l = 1
  • Type (z) — 4 lobes, daisy-shaped (d); l = 2

Using those l values, you can figure out the possible ml values for each type:

  • Type (x) = s orbital: l = 0; ml must be 0
  • Type (y) = p orbital: l = 1; ml can be -1, 0, or +1
  • Type (z) = d orbital: l = 2; ml can be -2, -1, 0, +1, or +2

Answer:

  • Type (x) — l = 0; ml must be 0
  • Type (y) — l = 1; ml can be -1, 0, or +1
  • Type (z) — l = 2; ml can be -2, -1, 0, +1, or +2

 

Check Your Work

Summary of what we would expect based on the related chemistry theory.

Show/Hide Watch Out!

Review the atomic orbital shapes and their characteristics (s-, p-, and d-orbitals) as well as which combinations of quantum numbers are and are not allowed to exist.

Recall the related fundamental principles that guide atomic orbital theory:

  • Pauli Exclusion Principle — no two electrons can have the same 4 quantum numbers.
  • Aufbau’s Principle — electrons occupy the lowest energy orbital available first.

Does your answer make chemical sense?

Show/Hide Answer

For question b, our answers on the number of orbitals in a sublevel make sense because:

  • An s-orbital (sphere-shaped electron density cloud) is an identical sphere regardless of its orientation in space, resulting in only 1 possible s-orbital at each energy level.
  • A p-orbital (propellor-shaped electron density cloud) can exist in3 different axes in 3-dimensional space; it can lay along the x-axis, y-axis, and z-axis, resulting in 3 possible p-orbitals (px, py, and pz) at each energy level.

PASS Attribution

Media Attributions

All figures by the authors (Brewer S. and Blackstock L.) are free to use under a CC0 license.

References

1. Thompson Rivers University. 2.4: Quantum Mechanics and The Atom. In CHEM 1500: Chemical Bonding and Organic Chemistry. LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/CHEM1500%3A_Chemical_Bonding_and_Organic_Chemistry/02%3A_Quantum_Theory_and_Electronic_Structure_of_Atoms/2.02%3A_Atomic_Spectroscopy_and_The_Bohr_Model.

2. OpenStax. 2.6: Electronic Structure of Atoms (Electron Configurations). In CHEM 1500: Chemical Bonding and Organic Chemistry. LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/CHEM_1500%3A_Chemical_Bonding_and_Organic_Chemistry/02%3A_Quantum_Theory_and_Electronic_Structure_of_Atoms/2.06%3A_Electronic_Structure_of_Atoms_(Electron_Configurations)

3. Thompson Rivers University. 2.5: The Shape of Atomic Orbitals. In CHEM 1500: Chemical Bonding and Organic Chemistry. LibreTexts, 2022. https://chem.libretexts.org/Courses/Thompson_Rivers_University/CHEM_1500%3A_Chemical_Bonding_and_Organic_Chemistry/02%3A_Quantum_Theory_and_Electronic_Structure_of_Atoms/2.05%3A_The_Shape_of_Atomic_Orbitals

4. Blackstock, L.; Brewer, S.; Jensen, A. PASS Chemistry Book CHEM 1500; LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/PASS_Chemistry_Book_CHEM_1500.

5. Blackstock, L.; Brewer, S.; Jensen, A. 2.3: Question 2.E.40 PASS – Quantum Numbers, Orbital Characteristics. In PASS Chemistry Book CHEM 1500. LibreTexts, 2023. https://chem.libretexts.org/Courses/Thompson_Rivers_University/PASS_Chemistry_Book_CHEM_1500/02%3A_Quantum_Theory_and_Electronic_Structure/2.03%3A_Question_2.E.40_PASS_-_quantum_numbers_orbital_characteristics.

6. OpenStax. 6.E: Electronic Structure and Periodic Properties (Exercises). In Chemistry 1e (OpenSTAX). LibreTexts, 2023. https://chem.libretexts.org/Bookshelves/General_Chemistry/Chemistry_1e_(OpenSTAX)/06%3A_Electronic_Structure_and_Periodic_Properties/6.E%3A_Electronic_Structure_and_Periodic_Properties_(Exercises)

7. Flowers, P.; Robinson, W. R.; Langley, R.; Theopold, K. Ch. 6 Exercises. In Chemistry 2e; OpenStax, 2019. https://openstax.org/books/chemistry-2e/pages/6-exercises

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

PASSchem Copyright © 2025 by Sharon Brewer, Lindsay Blackstock, TRU Open Press is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book